
中大新聞網訊(通訊員李冠中、吳曉鴻)近日,來自中山大學計算機學院量子計算與軟件研究所的研究成果論文“Recovering the Original Simplicity: Succinct and Deterministic Quantum Algorithm for the Welded Tree Problem(返璞歸真:求解焊接樹問題的簡潔與確定性量子算法)”被國際頂級學術會議SODA錄用。中山大學計算機學院為該論文的唯一署名單位,論文作者按字母序為:Guanzhong Li(李冠中)、Lvzhou Li(李綠周)、Jingquan Luo(羅鏡泉),其中李冠中和羅鏡泉分別為李綠周教授團隊的博士研究生和碩士研究生。
該論文重新審視了在量子算法領域備受關注的焊接樹問題,基于硬幣量子游走模型設計了求解該問題的具有指數加速優勢的簡潔確定性量子算法。這不僅打破了硬幣量子游走只能實現比經典算法平方加速的刻板印象,而且為簡化現有的基于量子游走的算法提供了新思路。據統計,這是SODA歷史上首篇署名單位完全來自中國大陸研究機構的專注于量子算法的論文。
焊接樹問題是少數幾個基于量子游走展現出量子指數加速優勢的問題。形象地說,該問題是要從迷宮入口找到出口,每走一步只能探索周邊有路徑相連的位置。這里的“迷宮”是兩棵深度為n的完全二叉樹,它們水平相對放置,中間的葉子左右隨機交替“焊接”起來形成一個回路,如下圖中虛線所示。假設“迷宮”的信息存放在一張鄰接表中。那么,在“迷宮”中每走一步,都需要訪問一次鄰接表以獲取當前位置的相鄰信息。焊接樹問題即要求盡可能少地訪問鄰接表從入口找到出口,其中訪問鄰接表的次數稱為查詢復雜度。可以證明針對該問題的任何經典算法的查詢復雜度都是n的指數量級,即為 Ω(2n)。
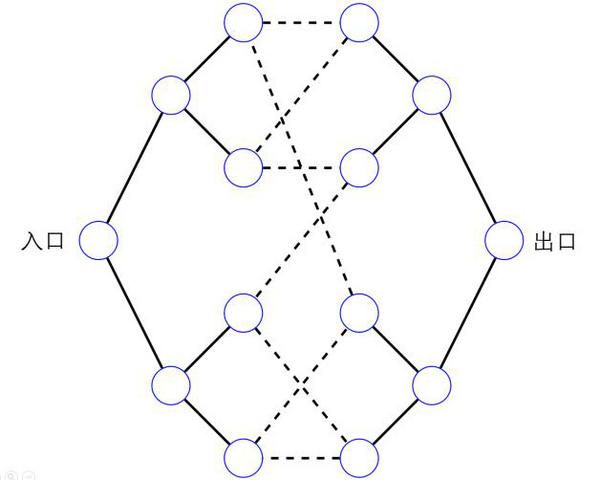
深度n=2的焊接樹
針對焊接樹問題,上述論文基于簡單直觀的硬幣量子游走模型設計了簡潔而高效的確定性量子算法。該工作價值體現在以下幾點:(1)與Jeffery 和 Zur(STOC'2023)的算法相比,所得的量子算法相當簡單,這不僅打破了硬幣量子游走只能實現比經典算法二次方加速的刻板印象,而且還展示了最簡量子游走模型的威力;(2) 所得的量子算法理論上可以百分之成功,而已有量子算法不可避免地具有失敗概率。這也可能改變人們這樣的看法:由于量子力學本質上是隨機的,不可能存在具有指數加速的確定性量子算法求解焊接樹問題;(3)文中展現的簡潔的算法思路具有很強的啟發意義。如同一位審稿人所說:“這篇論文可能會開創一條新的研究路線,簡化現有基于量子游走的算法,并提高它們的效率”。
據悉,SODA(ACM-SIAM Symposium of Discrete Algorithms)是算法領域的國際頂級會議,主要關注解決離散問題的高效算法和相關數據結構的研究,與 STOC、FOCS 一起被公認為理論計算機科學的三大頂級學術會議,在計算機科學領域享有崇高的聲望。
文稿終審:計算機學院 馬嘯