
心理學系潘俊豪副教授等通過把機器學習中Lasso (Least Absolute Shrinkage and Selection Operator )正則化算法和心理學領域的經典模型驗證性因素分析模型(Confirmatory Factor Analysis,CFA)結合,成功建立了帶局部項目依賴的CFA模型,在貝葉斯方法的框架下,對項目測量誤差之間的協方差使用雙指數先驗分布(如下圖),解決了在運用CFA模型分析心理學實際數據過程中數據出現違反“局部獨立性”假設時應如何建模的問題。 該研究近日發表于心理學頂級期刊《心理學方法》(Psychological Methods)。
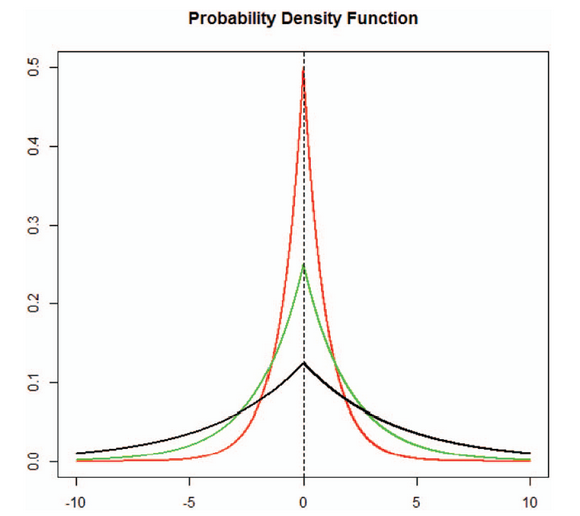
不同收縮參數下雙指數分布的概率密度函數
驗證性因素分析模型廣泛應用于心理學、社會學等領域的科學研究當中,以研究指標變量(Indicator)和潛變量(Latent Variable)之間的關系。在建模過程中,CFA模型(以及其他潛變量模型)的一個重要前提假設是局部獨立性(Local Independence),違反局部獨立性假設的情況稱為局部項目依賴。在實際數據分析當中,研究者往往默認局部獨立性假設成立從而建立測量模型。然而,隨著研究的深入,研究者逐漸意識到錯誤地假設局部獨立性會對研究結果(特別是估算潛變量之間的關系)產生嚴重的誤導。作為最基礎的潛變量模型之一,在CFA模型的統計分析中如何有效地考慮指標變量間的局部依賴程度并研究相應的統計分析方法一直是學界關注的熱點問題。此問題的解決將有助于解決其他潛變量模型中不滿足局部獨立性時應如何建模的問題。潘俊豪副教授等的研究成果為此提供了新的研究思路。
《心理學方法》(Psychological Methods)時任副主編賓夕法尼亞州立大學Sy-Miin Chow教授認為該成果“能為CFA模型的研究做出有價值的貢獻(a valuable contribution)”;其他匿名評審者認為“把貝葉斯Lasso先驗應用于CFA建模是一個偉大的想法(a very great idea)”,“解決了CFA使用過程中一個重要的問題(an important issue)”。
《心理學方法》(Psychological Methods)由美國心理學會出版,是心理學,特別是心理學研究方法領域頂級期刊,SSCI收錄,2016年影響因子4.667,5年影響因子10.141。據悉,這是心理學系教師在該刊發表的第一篇第一作者論文,也是第二篇大陸高校學者第一作者論文。
文章來源:
Pan, J., Ip, E. H., & Dubé, L. (2017). An alternative to post hoc model modification in confirmatory factor analysis: The Bayesian lasso. Psychological Methods, 22(4), 687-704. http://dx.doi.org/10.1037/met0000112