
11月5日,美國科學院院刊(PNAS)在線發表了我校數學學院張家軍副教授和周天壽教授的最新研究論文“Markovian Approaches to Modeling Intracellular Reaction Processes with Molecular Memory”。張家軍副教授為論文的第一作者,周天壽教授為論文的通訊作者,中山大學為唯一作者單位。
該研究解決了生化反應系統(包括生物分子網絡)研究領域中的一個長期未解決的問題,即如何建模和分析帶有分子記憶的生化反應系統。為此,作者創新性地建立起一套實用理論,其核心是靜態廣義化學主方程,它把一個非馬氏問題轉化為一個馬氏問題,并由此揭示出非馬氏生化反應系統的本質特性。
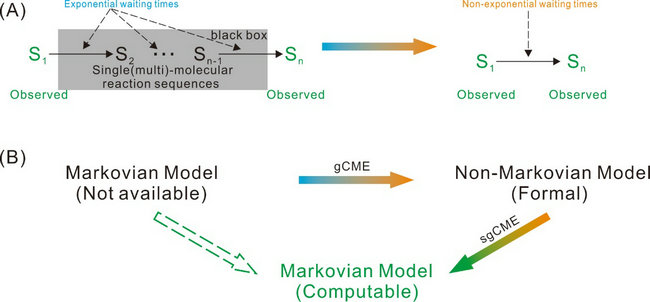
非馬氏生化反應系統可有效轉化為馬氏生化反應系統進行建模與分析
長期以來,生化反應系統的建模與分析依賴于馬氏假設,即反應物的隨機運動不受以前狀態的影響,而僅受當前狀態的影響。然而,這種無記憶的假設是非常理想化的,實際的反應系統是帶有記憶的,例如許多生物學實驗已經證實:分子記憶廣泛存在于基因表達調控系統中,并對基因表達水平有重要影響。由于分子記憶能夠導致非馬氏反應運動學,以及由于經典的馬氏理論不能夠直接應用于非馬氏反應過程的建模與分析,從而導致許多理論挑戰。經過對非馬氏生化反應系統的多年研究,作者建立起一套實用的理論與方法,主要包括靜態廣義化學主方程(stationary generalized chemical master equation)、靜態廣義福克-普朗克方程(stationary generalized Fokker-Planck equation)和靜態廣義線性噪聲逼近(generalized linear noise approximation),揭示出:盡管各個反應物的暫態動力學可能是非馬氏的,但生化反應系統的整個微觀變量隨時間演化最后都變成馬氏變量,不管反應網絡的拓撲如何復雜以及不管特征化分子記憶的等待時間分布的形式如何復雜。這三種一般性格式開辟了研究復雜生物分子系統的新方向,具有寬廣的應用前景,特別是能夠幫助人們發現新的生物學知識。
該研究工作得到了國家自然科學基金、廣州市科技計劃項目、廣東省重點領域研發計劃項目,以及中山大學廣東省計算科學重點實驗室的大力支持。