
中大新聞網訊(通訊員雷世菁)近日,中山大學物理學院姚道新教授團隊在量子相變的無序算符標度行為研究中取得重要進展,在國際上首先提出無序算符可以用來探測邊界態和邊界的臨界行為,并分析了其標度行為。2024年5月17日,該成果以“Measuring the Boundary Gapless State and Criticality via Disorder Operator”為題,以中山大學為第一單位發表在國際著名物理刊物《物理評論快報》 (Physical Review Letters 132, 206502 (2024)),并獲得編輯推薦(Editor’s suggestion)。
量子相變一直是凝聚態物理中重要且有趣的主題之一。晶格系統的邊界由于其配位數的不同展現出比體內更加豐富的相變行為,即表面臨界行為。由于邊緣模與體的臨界漲落耦合在一起,邊界會誘導出新奇的相變行為,吸引了眾多研究人員的關注。如何在多體計算中,提取邊界臨界行為的信息,進一步驗證表面臨界理論的可靠性,比如邊界共形場論(BCFT),是量子多體計算重要的方向。
另外一方面,近年來非局域算符的研究逐漸興起,它們可以從廣義的對稱性和domain wall的角度去理解物相和相變。無序算符作為一種非局域的測量算符,能夠揭示相和相變點的高價對稱性和共形場論信息,從全局的角度理解相變普適類的信息。例如,在S=1/2的二維正方晶格J1-J2柱狀海森堡模型中,能夠提取出O(3)相變點的流中心荷CJ,反映其普適類信息。
姚道新教授團隊率先利用無序算符對二維具有對稱性保護拓撲相(SPT)的AKLT模型的邊界性質進行了研究。在AKLT相,邊界的自旋形成有效的海森堡鏈。無序算符能夠反映邊緣態的物理性質,提取海森堡鏈的Luttinger參數,揭示(1+1)維邊界SU(2)1的物理。當體系靠近相變點時,無能隙的邊緣模與體的臨界漲落逐漸耦合在一起,無序算符不但能夠反映邊緣態的(1+1)維的SU(2)1物理,提取Luttinger參數,還能夠提取體的臨界行為O(3)臨界模的共形場論信息。
在此基礎上,姚道新教授團隊對無序算符的標度行為提出一個猜想。在臨界點處,無能隙邊緣模和體的臨界模會以疊加的形式進入到無序算符的標度行為中,體現在其對數項中,它們遵從以下公式。
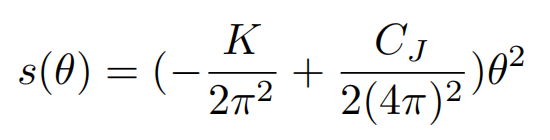
其中的K項由無能隙的邊緣態提供,而CJ項由體的O(3)臨界模貢獻。數值結果很好地驗證了猜想的可靠性,從數值角度直觀揭示了邊緣模與體的臨界漲落耦合的物理圖像。
進一步,姚道新教授團隊利用量子蒙特卡洛方法研究了二維AKLT模型的糾纏譜和能譜的對應關系。著名的Li-Haldane猜想指出在拓撲態里面糾纏譜的低能部分和開邊界的能譜具有一一對應的關系。研究團隊發現,在AKLT模型邊界施加微擾,其糾纏譜和能譜并不總是具有對應關系;在某些情況下,即使邊界變成有能隙的,其糾纏譜和能譜也具有對應關系。研究團隊利用新的蟲洞圖像很好地解釋了這些數值結果,并揭示了蟲洞圖像可以成為理解復雜系統糾纏譜變化的強有力的工具。相關工作已經發表在Physical Review B刊物上(Phys. Rev. B 109, 094416(2024))。 在此之前,姚道新教授團隊利用量子蒙特卡洛方法研究了該模型體和邊界的激發譜,為理解對稱保護拓撲相和磁有序的激發提供了重要的數值依據(Phys. Rev. B 105, 014418 (2022))。并且,姚道新教授團隊還對S>1/2的二維四八晶格海森堡模型的相圖和激發譜進行了細致的計算和研究(Phys. Rev. B 106, 085101 (2022))。
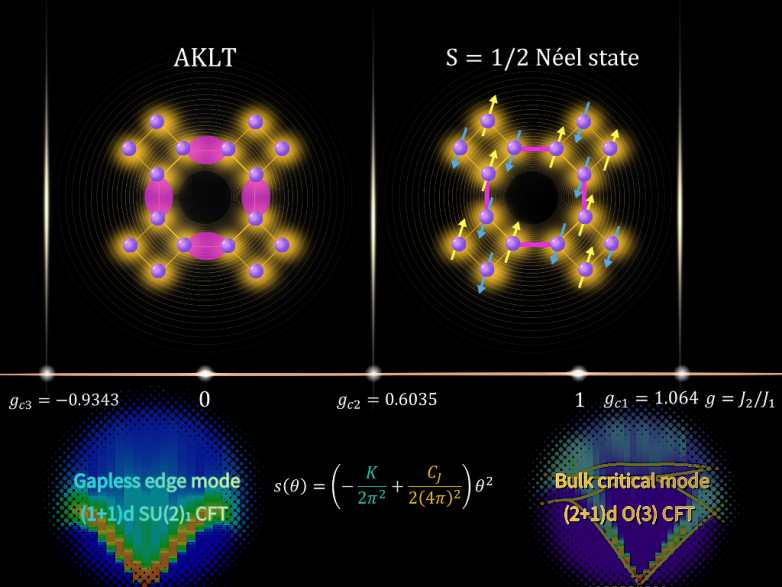
S=1/2的J1-J2四八晶格海森堡模型的相圖,無序算符反映了臨界點處邊緣模和體的臨界模耦合在一起的物理信息。
中山大學物理學院博士研究生劉澤楠為論文的第一作者,中山大學物理學院教授姚道新、西湖大學研究員嚴正和北京航空航天大學杭州國際創新研究院副教授王艷成為論文的通訊作者,比利時根特大學博士后黃瑞珍參與了本研究的理論工作。中山大學的理論研究工作依托物理學院公共科研平臺和中子科學平臺、廣東省磁電物性分析與器件重點實驗室、光電材料與技術國家重點實驗室、高等學術研究中心;計算工作依托中山大學國家超級計算廣州中心。上述工作得到國家重點研發計劃、國家自然科學基金等的資助。
論文鏈接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.206502